La formule d'écoulement, ou le problème du bassin qui se vide par gravité
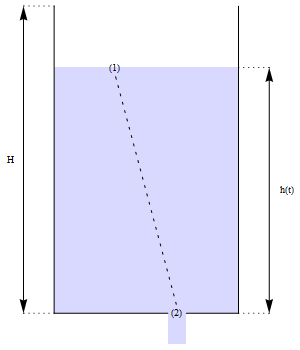
Qu'il s'agisse d'un bassin, d'un réservoir ou d'une cuve, nous supposons que son contenu liquide s'en échappe par un trou sous l'effet de la gravité.
Sachant qu'un bassin se vide en 100 minutes, combien de temps faut-il pour qu'il se vide de moitié ?
Ne répondez pas 50 minutes ! En effet, lorsque le bassin est plein, la pression sur le trou de sortie est grande. Au début, le bassin se vide rapidement. Par contre, lorsqu'il est bientôt vide, la pression sur le trou de sortie devient faible. Ainsi, vers la fin, le bassin se vide lentement. Dans ces circonstances, il serait aberrant de résoudre le problème au moyen d'une fonction affine.
Nous donnons ci-dessous les formules et les tabelles qui mettent en rapport
- le taux de remplissage du bassin (ou le pourcentage du volume restant), noté η
- la fraction de la durée de la vidange (ou pourcentage de la durée), noté τ
Vous y trouverez la réponse à la question posée, à savoir 29.3 minutes.
Volume restant en fonction de la durée de la vidange
|
τ durée |
η volume restant η = (1 - τ)2 |
| 0 % | 100 % |
| 10 % | 81.0 % |
| 20 % | 64.0 % |
| 30 % | 49.0 % |
| 40 % | 36.0 % |
| 50 % | 25.0 % |
| 60 % | 16.0 % |
| 70 % | 9.0 % |
| 80 % | 4.0 % |
| 90 % | 1.0 % |
| 100 % | 0.0 % |
Durée de la vidange en fonction du volume restant
|
η volume restant |
τ durée τ = 1 - √η |
| 100 % | 0.0 % |
| 90 % | 5.1 % |
| 80 % | 10.6 % |
| 70 % | 16.3 % |
| 60 % | 22.5 % |
| 50 % | 29.3 % |
| 40 % | 36.8 % |
| 30 % | 45.2 % |
| 20 % | 55.3 % |
| 10 % | 68.4 % |
| 0 % | 100.0 % |
Justification avec calculs détaillés (équation de Bernoulli)