«Surface du cercle» et autres erreurs de formulation en géométrie
Cette figure n'est pas un rectangle, mais un carré.
Cet énoncé est absurde car un carré est un rectangle dont deux côtés consécutifs sont égaux.
Reformulation correcte: Cette figure est non seulement un rectangle, mais un carré.
Illustration: un carré considéré comme un membre d'une famille de rectangles:





Cette figure n'est pas un losange, mais un carré.
Cet énoncé est absurde car un carré est un losange dont deux côtés consécutifs sont perpendiculaires.
Reformulation correcte: Cette figure est non seulement un losange, mais un carré.
Illustration: un carré considéré comme un membre d'une famille de losanges:





Cette figure n'est pas un parallélogramme, mais un rectangle.
Cet énoncé est absurde car un rectangle est un parallélogramme dont deux côtés consécutifs sont perpendiculaires.
Reformulation correcte: Cette figure est non seulement un parallélogramme, mais un rectangle.
Illustration: un rectangle considéré comme un membre d'une famille de parallélogrammes:





Cette figure n'est pas un trapèze, mais un rectangle.
Cet énoncé est absurde car un rectangle est un trapèze dont les paires de côtés consécutifs sont perpendiculaires.
Reformulation correcte: Cette figure est non seulement un trapèze, mais un rectangle.
Illustration: un rectangle considéré comme un membre d'une famille de trapèzes rectangles:
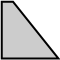




La base d'un triangle est de 3 m et la hauteur est de 2 m.
La formulation est fautive: l'expression «la base» suggère qu'il n'y en a qu'une, alors qu'il y en a trois; de même pour «la hauteur». Il est ainsi important de savoir s'il s'agit de la hauteur qui correspond à la base donnée.
Par ailleurs, la base et la hauteur ne sont pas des nombres réels, mais des segments, c'est-à-dire des ensembles de points du plan.
Reformulation correcte: Une base d'un triangle mesure 3 m, et la hauteur correspondante mesure 2 m.
Un rectangle de (3 m)×(12 m) et un carré de (6 m)×(6 m) sont des surfaces égales.
Pour illustrer concrètement la notion de surface, découper dans une feuille de papier, avec une paire de ciseaux, un rectangle de (3 cm)×(12 cm) et un carré de (6 cm)×(6 cm). Les deux surfaces ne coïncident pas.
C'est faux. Une surface est une portion de plan. Deux surfaces sont égales si on peut les superposer par des translations et des rotations. En particulier, deux surfaces égales ont la même forme.
Reformulation correcte: Un rectangle de (3 m)×(12 m) et un carré de (6 m)×(6 m) ont la même aire. Une aire est un nombre réel non négatif qui mesure une surface.
Quelle est l'aire A d'un cercle de rayon r ?
Réponse incorrecte: A = π r2
Le cercle étant une ligne, son épaisseur est nulle et son aire est nulle. Réponse correcte: A = 0
Quelle est la surface S d'un disque de rayon r ?
Réponse incorrecte: S = π r2
La surface étant une portion de plan, elle ne peut pas être égale à un nombre réel, car ce sont des objets de natures différentes.
Quelle est l'aire A du disque de rayon r ?
Réponse correcte: l'aire A du disque de rayon r est A = π r2