Démocratie: la préférence n'est pas transitive

Une transitivité problématique

Si un corps électoral préfère le candidat A au candidat B et le candidat B au candidat C, le sens commun semble indiquer que A est préféré à C. Cependant, ce genre de raisonnement «logique» n'a pas cours en matière de mathématiques électorales.

L'exemple d'une votation démocratique

Pour trois candidats A, B, C, des élections ont montré que

A est préféré à B et
B est préféré à C.

Peut-on conclure que A est préféré à C ?

Une votation ultérieure à l'issue de laquelle C serait préféré à A indiquerait-elle que les électeurs auraient changé d'opinion ?

Supposons que

• 1/3 des électeurs classent les candidats dans l'ordre de préférence A, B, C;
• 1/3 des électeurs classent les candidats dans l'ordre de préférence B, C, A;
• 1/3 des électeurs classent les candidats dans l'ordre de préférence C, A, B;

et qu'ils ne changent plus d'opinion.

• À la question «Préférez-vous A ou B ?», A obtient 2/3 des voix.
• À la question «Préférez-vous B ou C ?», B obtient 2/3 des voix.
• À la question «Préférez-vous C ou A ?», C obtient 2/3 des voix.

Il se peut donc que C soit préféré à A sans que les électeurs aient changé d'opinion.

Représentation graphique

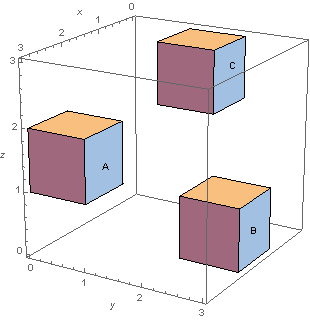
• Le premier groupe d'électeurs ordonne {C, B, A} selon l'axe des x. Le préféré est A.
• Le deuxième groupe d'électeurs ordonne {A, C, B} selon l'axe des y. Le préféré est B.
• Le troisième groupe d'électeurs ordonne {B, A, C} selon l'axe des z. Le préféré est C.

Le paradoxe de Condorcet

Il s'agit du paradoxe de Condorcet dont une autre forme est le jeu «papier-caillou-ciseaux»: si le papier gagne contre le caillou et que le caillou gagne contre les ciseaux, on ne doit pas en déduire que le papier gagne contre les ciseaux. On dit que la relation binaire «.. est préféré à ..» ou «.. gagner contre ..» est non transitive.

Voilà qui complique singulièrement l'exercice de la démocratie ! Il faut en tenir compte lors des élections, des votations, des enquêtes et des sondages d'opinion. En particulier,

on ne peut pas éviter de poser des questions qui semblent redondantes, mais qu'on ne peut pas remplacer par un «raisonnement».

Il est bien connu qu'une part du pouvoir démocratique appartient à ceux qui formulent les questions à leur avantage.