Loi de la vitesse moyenne d'Oresme
Cinématique
Nicole Oresme (1320 - 1382), maître de l'université de Paris
Sa loi de cinématique «Loi du degré moyen d'Oresme» est reformulée ici en langage contemporain.
Loi de la vitesse moyenne
Pour un corps en mouvement uniformément accéléré (c'est-à-dire dont la vitesse varie régulièrement), sa vitesse moyenne (c'est-à-dire la vitesse constante qui lui ferait parcourir la même distance dans le même temps) est égale à la moyenne arithmétique des vitesses initiale et finale.
Notations
\( d \quad \) distance parcourue durant l'intervalle de temps \( [ t_0; t_1 ] \);
\( \Delta t = t_1 - t_0 \quad \) durée du mouvement;
\( \overline{v} = \frac{d}{\Delta t} \quad \)vitesse moyenne sur l'intervalle de temps \( [ t_0; t_1 ] \);
\( v(t) \quad \) vitesse à l'instant \( t \) (la fonction \( v(t) \) est affine);
\( v(t_0) \quad \) vitesse initiale;
\( v(t_1) \quad \) vitesse finale.
Formule
\[ \overline{v} = \frac{v(t_0) + v(t_1)}{2} \]Modèle géométrique pour une vitesse constante
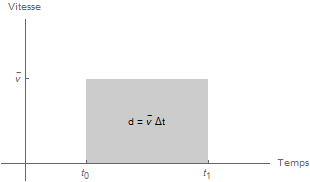
Dans un graphique, reportons le temps sur l'axe horizontal et la vitesse sur l'axe vertical.
Pour calculer la distance parcourue, on multiplie la vitesse par la durée. Donc, la distance parcourue est représentée par l'aire du rectangle:
Modèle géométrique pour un mouvement uniformément accéléré
La vitesse varie régulièrement. La distance parcourue est représentée par l'aire du trapèze rectangle:
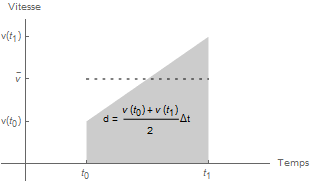
Démonstration géométrique de la loi de la vitesse moyenne
Pour la vitesse moyenne
\[ \overline{v} = \frac{v(t_0) + v(t_1)}{2} \]les deux aires sont égales.
Un point de vue fertile
Cette idée fertile a été développée par Jean de Buridan, Thomas Bradwardine, Galilée, etc. Dans la physique contemporaine, cette représentation est au centre du calcul intégral.